- Introduction
- Multiplication en colonne à 1 chiffre
- Multiplication en colonne à deux (2) chiffres
- Apprendre à multiplier avec retenue
- Multiplication avec plusieurs retenues et à 2 chiffres 425 x 23
- Un autre exemple un peu plus compliqué : multiplication 345 x 623 avec la méthode scolaire
- Toutes les différentes façons de multiplier des nombres
- Révisez vos tables de multiplication
Introduction
Cet article explique la méthode scolaire pour poser une multiplication, c'est la méthode enseignée à l'école. Cette méthode de multiplication est surnommée multiplication en colonne.
Je vais vous montrer plusieurs exemples, le premier est très simple (sans retenue) mais c'est pour bien comprendre le principe, les suivants seront un peu plus compliqués.
Multiplication en colonne à 1 chiffre
Diaporama
Nous voulons multiplier 12 par 4 (12 x 4) et connaître le résultat de cette multiplication.
Voici un diaporama vous montrant comment multiplier avec cette technique de multiplication. Pour visualiser le diaporama, il suffit de cliquer sur les flèches. Pas d'inquiétude, tout sera détaillé dans la suite de cet article.
Détails
Nous voulons multiplier 12 par 4 (12 x 4) et connaître le résultat de cette multiplication.
1) La question du jour notée sur 20 points : combien font 12 x 4 (12 multiplier par 4)?

2) On pose la multiplication : on écrit le 12, puis on écrit le 4 aligné tout à droite, on tire un joli trait et on dessine le signe de multiplication.

3) On multiplie 4 x 2 (c'est-à-dire le chiffre des unités du bas multiplié par le chiffre des unités du haut).

4) Et on écrit le résultat de cette petite multiplication : 4 x 2 = 8

5) On multiplie en suite le 4 par le 1 (c'est-à-dire le chiffre des unités du bas multiplié par le chiffre des dizaines du haut).

6) Et on écrit le résultat de cette petite multiplication : 4 x 1 = 8

7) Le résultat final est donc : 12 x 4 = 48

Multiplication en colonne à deux (2) chiffres
Diaporama
Maintenant que vous avez appris la multiplication en colonne à 1 chiffre, passons maintenant à 2 (deux) chiffres. C'est exactement le même principe sauf qu'il faudra "sauter une ligne" et faire une addition.
Voici un diaporama vous montrant comment multiplier avec cette technique de multiplication. Pour visualiser le diaporama, il suffit de cliquer sur les flèches. Pas d'inquiétude, tout sera détaillé dans la suite de cet article.
Détails
Nous voulons multiplier 122 par 32 (122 x 32) et connaître le résultat de cette magnifique multiplication.
1) On écrit le premier nombre (122), on écrit le deuxième nombre (32) que l'on aligne bien tout à droite (les chiffres des unités des deux nombres sont donc bien alignés. On trace un trait, et on dessine le symbole "multiplier" (X)
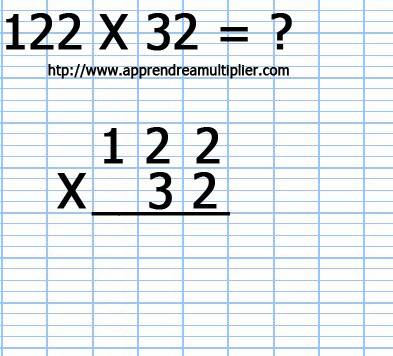
2) On multiplie le chiffre des unités (2) du deuxième nombre (32) par le chiffre des unités (2) du premier nombre (122). Cela nous sonne 2x2=4 et l'on écrit le résultat (4).
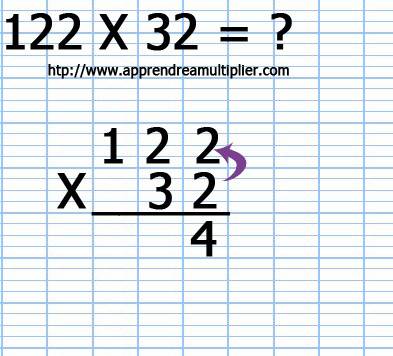
3) On multiplie le chiffre des unités (2) du deuxième nombre (32) par le chiffre des dizaines (2) du premier nombre (122). Cela nous sonne 2x2=4 et l'on écrit le résultat (4).
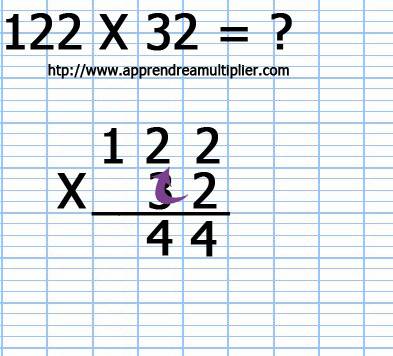
4) On multiplie le chiffre des unités (2) du deuxième nombre (32) par le chiffre des centaines (1) du premier nombre (122). Cela nous sonne 2x1=2 et l'on écrit le résultat (2).
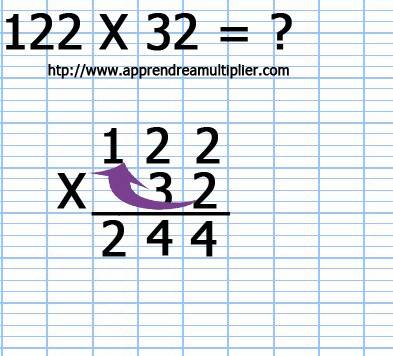
5) La première ligne est remplie. Attention, maintenant, il faut sauter une ligne et se décaler vers la gauche, et c'est pour cela que nous écrivons un point pour ne pas se tromper.
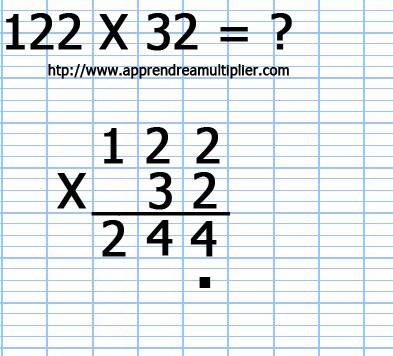
6) On multiplie le chiffre des dizaines (3) du deuxième nombre (32) par le chiffre des unités (2) du premier nombre (122). Cela nous sonne 3x2=6 et l'on écrit le résultat (6).
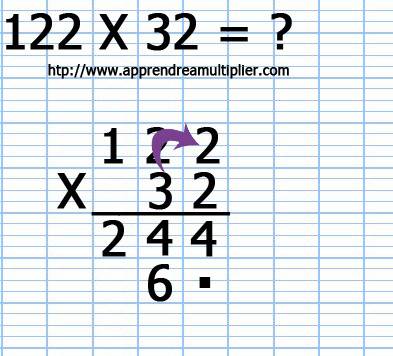
7) On multiplie le chiffre des dizaines (3) du deuxième nombre (32) par le chiffre des dizaines (2) du premier nombre (122). Cela nous sonne 3x2=6 et l'on écrit le résultat (6).
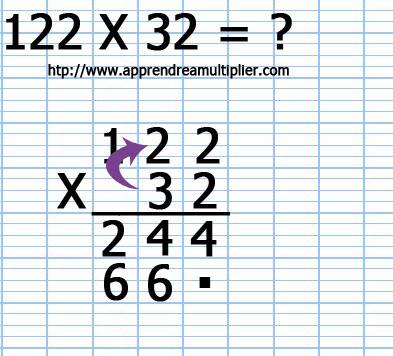
8) On multiplie le chiffre des dizaines (3) du deuxième nombre (32) par le chiffre des centaines (1) du premier nombre (122). Cela nous sonne 3x1=3 et l'on écrit le résultat (3).
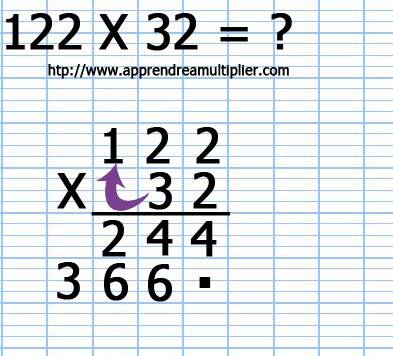
9) Voici venue maintenant l'heure de l'addition : on tire un joli trait et on écrit le symbole "+" et on se prépare maintenant à additionner les deux nombres que nous avons trouvés
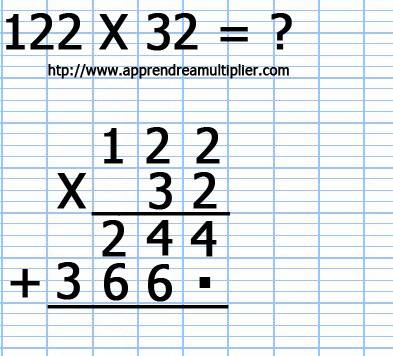
10) L'addition est la suivante : 244 + 3660 = 3904 (on peut remplacer le point par un zéro). Donc 122x32 = 3904
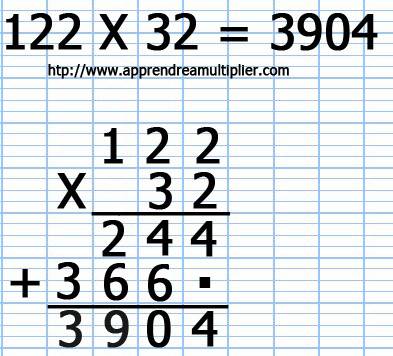
Résumé
Les deux précédentes multiplications étaient relativement assez simples, car il n'y avait pas de retenues. Les retenues apparaissent lorsque le résultat d'une multiplication entre les deux chiffres dépasse 9 (c'est-à-dire un résultat à 2 chiffres)
Apprendre à multiplier avec retenue
Diaporama
Voici un diaporama vous montrant comment multiplier avec cette technique de multiplication. Pour visualiser le diaporama, il suffit de cliquer sur les flèches. Pas d'inquiétude, tout sera détaillé dans la suite de cet article.
Détails
Voici en détail toutes les explications pour apprendre à multiplier en colonne avec une retenue :
1) On pose notre multiplication : on écrit le premier nombre (115), puis on écrit le deuxième nombre (4) bien aligné à droite. On tire un trait et inscrit le symbole de multiplication (X)
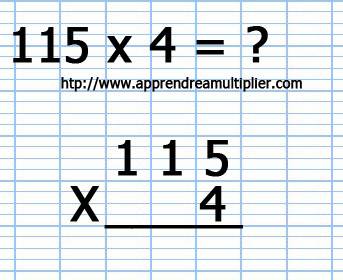
2) Il faut multiplier le chiffre des unités (4) du chiffre du bas (4) par le chiffre des unités (5) du chiffre du haut (115), ce qui donne 4 x 5 = 20. Mais l'on écrit par 20 en dessous du trait, on écrit seulement le 0 en bas et le 2 en haut, c'est la retenue car on retient ce nombre pour plus tard.
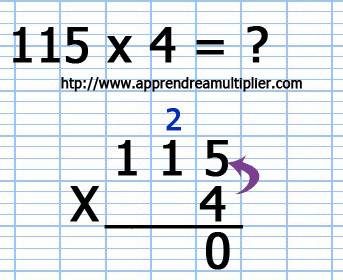
3) Il faut multiplier le chiffre des unités (4) du chiffre du bas (4) par le chiffre des dizaines (1) du chiffre du haut (115), ce qui donne 4 x 1 = 4, mais nous avons une retenue (le chiffre bleu 2), et il faut additionner donc le résultat est (4 x 1 ) + 2 = 6, donc on écrit 6

4) Il faut multiplier le chiffre des unités (4) du chiffre du bas (4) par le chiffre des centaines (1) du chiffre du haut (115), ce qui donne 4 x 1 = 4

5) Voici donc notre multiplication : 115 x 4 = 460

Résumé de notre multiplication avec retenue
Multiplication avec plusieurs retenues et à 2 chiffres 425 x 23
Diaporama
Maintenant que vous savez vous servir des retenues dans les multiplications en colonne, avec plusieurs chiffres, c'est exactement pareil.
Nous allons le voir tout de suite avec la multiplication 425 x 23
Voici un diaporama vous montrant comment multiplier avec cette technique de multiplication. Pour visualiser le diaporama, il suffit de cliquer sur les flèches. Pas d'inquiétude, tout sera détaillé dans la suite de cet article.
Détails
Voici en détails les explications d'une multiplication en colonne avec plusieurs retenues et 2 chiffres.
1) J'écris 435 puis 23 en faisant bien attention que les chiffres des unités (5 et 3) soient bien alignés à droite. Je tire un trait, et je note le signe X de multiplication.
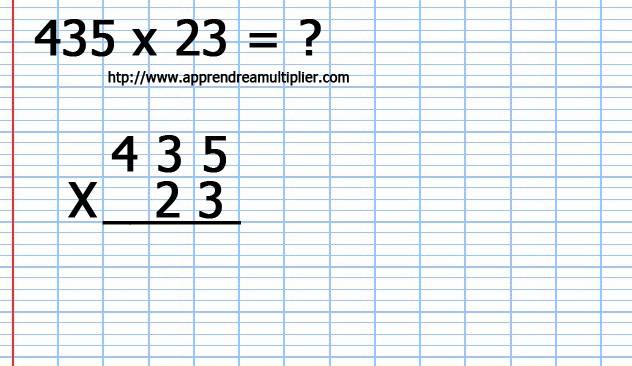
2) Je multiplie le chiffre des unités (3) du nombre du bas (23) par le chiffre des unités (5) du nombre du haut (435) : 3 x 5 = 15. Je pose le 5 et je retiens le 1.
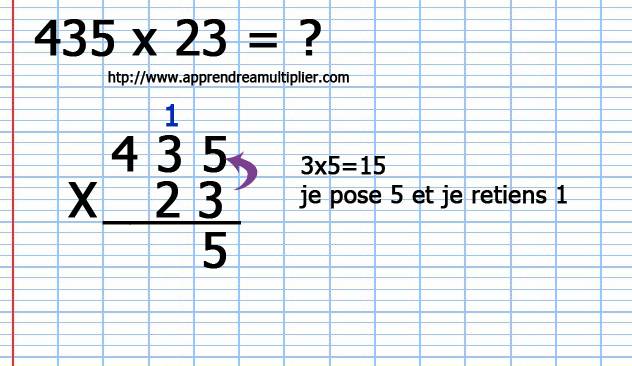
3) Je multiplie le chiffre des unités (3) du nombre du bas (23) par le chiffre des dizaines (3) du nombre du haut (435) et additionne la retenue (1) : (3 x 3 ) + 1 = 10. Je pose le 0 et je retiens le 1 (en bleu)
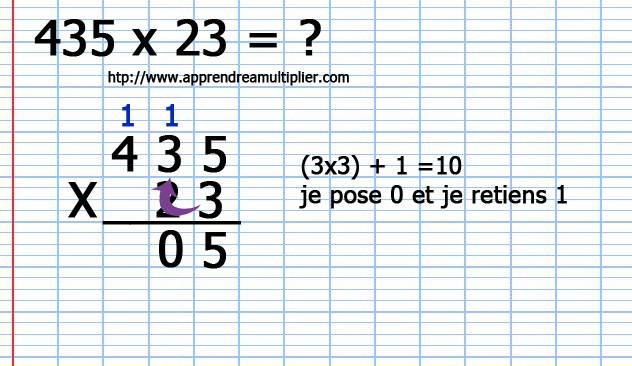
4) Je multiplie le chiffre des unités (3) du nombre du bas (23) par le chiffre des centaines (4) du nombre du haut (435) et j’additionne la retenue : ( 3 x 4 ) + 1 = 13 . Je peux poser directement le 13 sans écrire la retenue, car il nous avons terminé cette première ligne.

5) Je saute une ligne et écris un point pour me décaler à gauche et efface les retenues précédentes. Je multiplie le chiffre des dizaines (2) du nombre du bas (23) par le chiffre des unités (5) du nombre du haut (435) : 2 x 5 = 10 Je pose le 0 et je retiens 1

6) Je multiplie le chiffre des dizaines (2) du nombre du bas (23) par le chiffre des dizaines (3) du nombre du haut (435) et je rajoute la retenue : ( 2 x 3 ) + 1 = 7. J'écris donc le 7
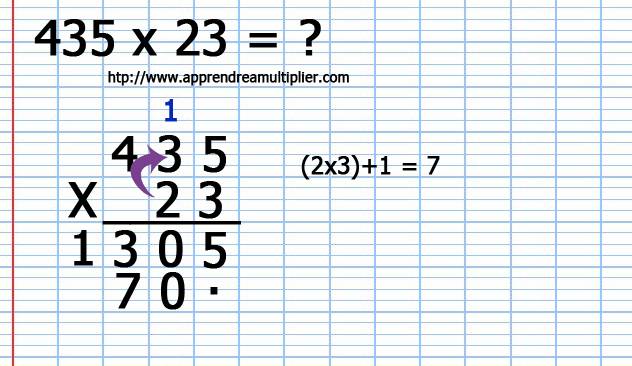
7) Je multiplie le chiffre des dizaines (2) du nombre du bas (23) par le chiffre des centaines (4) du nombre du haut (435) : 2 x 4 = 8 . J'écris le 8 et il n'y a pas de retenue.
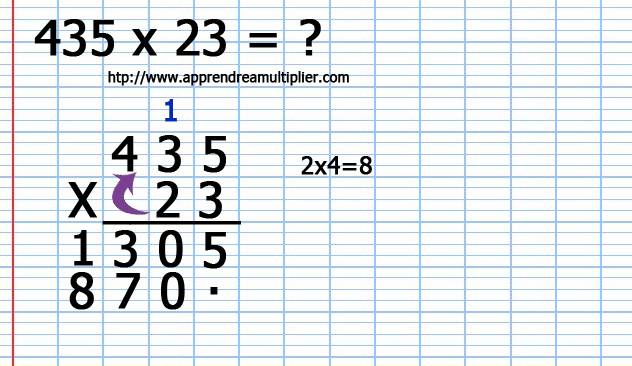
8) Je me prépare pour l’addition finale, je tire un trait et écrit le symbole + de notre addition.
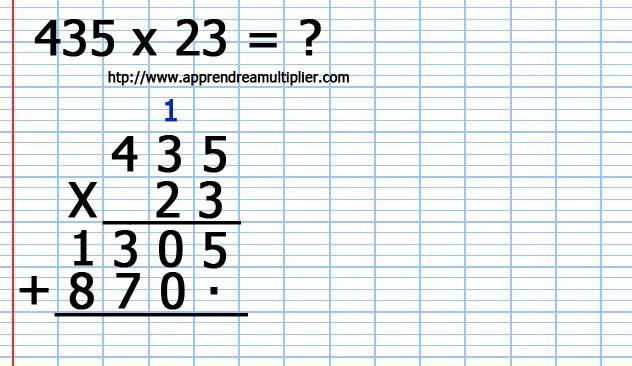
9) J’additionne 1305 + 870 et cela me donne 10005 donc 435 x 23 = 10005
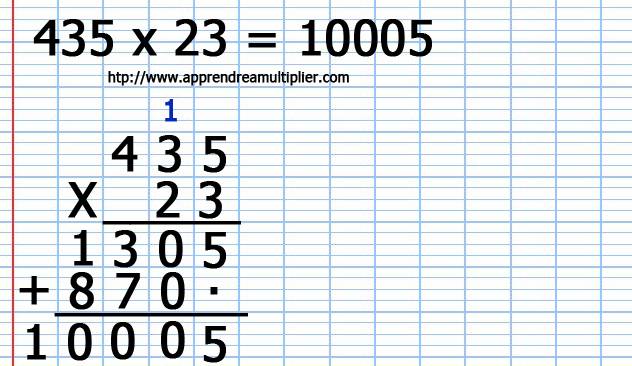
Résumé de notre jolie multiplication
Un autre exemple un peu plus compliqué : multiplication 345 x 623 avec la méthode scolaire
Diaporama
Nous allons apprendre à poser la multiplication trois cent quarante-cinq fois six cent vingt-trois (345 x 623).
Voici un diaporama vous montrant comment multiplier avec cette technique de multiplication. Pour visualiser le diaporama, il suffit de cliquer sur les flèches. Pas d'inquiétude, tout sera détaillé dans la suite de cet article.
Ddétails
1) Combien font 345 x 623 ?
- Je pose ma multiplication :
- J'aligne les 2 nombres à droite
- J'écris le signe de multiplication (x)
- Je trace un trait

2) 3 x 5 = 15
- Je pose 5 et je retiens 1. C'est-à-dire que je pose le chiffre des unités (5) et j'écris en retenue le chiffre des dizaines (1)

3) 3 x 4 = 12
- J'ajoute la retenue : 12 + 1 = 13
- Je pose 3 et je retiens 1

4) 3 x 3 = 9
- J'ajoute la retenue : 9 + 1 = 10
- Je pose 10 (je ne pose pas de retenue, car c'est la fin de la ligne)

5) Je pose un point lorsque je saute de ligne.
- 2 x 5 = 10
- Je pose 0 et je retiens 1

6) 2 x 4 = 8
- J'ajoute la retenue : 8 + 1 = 9
- Je pose 9

7) 2 x 3 = 6
- Je pose 6

8) la deuxième ligne est enfin terminée, je pose un point pour sauter de ligne

9) 6 x 5 = 30
- Je pose 0 et je retiens 3

10) 6 x 4 = 24
- J'ajoute la retenue : 24 + 3 = 27
- Je pose 7 et je retiens 2

11) 6 x 3 = 18
- J'ajoute la retenue : 18 + 2 = 20
- Je pose 20 (je ne retiens pas 0 car c'est la fin de la ligne)

12) Je me prépare à additionner les 3 nombres que je viens de trouver :
- Je trace un trait
- J'écris les signes + et le signe =

13) J'additionne les nombres trouvés :
- 1035 + 6900 + 207000 = 214935
Conclusion : 345 + 623 = 214935

Résumé de la multiplication 345 x 623 (animation)
Toutes les différentes façons de multiplier des nombres
Il existe plusieurs techniques pour multiplier deux nombres autres que la méthode que l'on apprend à l'école, voici différentes technique :

Poser une multiplication, la méthode scolaire
Poser une multiplication comme à l'école, la méthode scolaire traditionnellement enseignée par l'éducation nationale : Explication en image
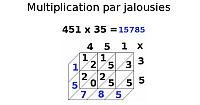
Multiplication par jalousies
Multiplication par jalousies : Une autre méthode pour multiplier deux nombres. Exemples et explications en image

Multiplication, technique Russe
Multiplication, technique Russe : Une autre méthode pour multiplier deux nombres. Explications détaillées en image.
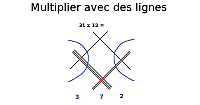
Multiplier avec des lignes
Multiplier avec des lignes : Une autre méthode pour multiplier deux nombres. explications de cette technique en image.
Révisez vos tables de multiplication
Voici les principales tables de multiplication :
- Table de multiplication de 0
- Table de multiplication de 1
- Table de multiplication de 2
- Table de multiplication de 3
- Table de multiplication de 4
- Table de multiplication de 5
- Table de multiplication de 6
- Table de multiplication de 7
- Table de multiplication de 8
- Table de multiplication de 9
- Table de multiplication de 10

Merci beaucoup pour ses fondamentaux qui,on ne va pas se mentir,s'étaient perdus dans les méandres de la vie actives !
Répondre à ce(s) commentaires(s)